I make my living working with ASP.NET sites, but I really like static web sites. That’s why I chose Jekyll for publishing this blog.

Old Build Process

I spend most of my time working on Windows. Jekyll and Windows can be made to play well together, but it isn’t easy or intuitive, and if you obsess over using the most recent versions of things, it gets complicated.

I got super excited when I was finally able to use the Windows Subsystem for Linux because I was able to edit my blog code in Windows, and run the Jekyll tools from Linux without having to run a VM or dual boot. But it’s still a lot more work than I’d like:

• Open Ubuntu
• Navigate to the Windows file system where I store my blog code
• jekyll build
• From a Windows command prompt, run my deploy script

New Build Process

This past weekend, I spoke at RevolutionConf. They had an afternoon Docker workshop, and I finally decided it was time to learn something about Docker because all the cool kids are using it.

Thanks to Docker, here’s my new build process:

• Run a batch file from a Windows command prompt

How Does It Work?

The Jekyll folks have a few official Docker images. I’m using the one with all the build tools.

First, I created a docker-compose.yml file in the root of my project:

jekyll:
    image: jekyll/builder
    command: jekyll serve --watch --incremental
    ports:
        - 4001:4001
    volumes:
        - .:/srv/jekyll

This file says:

• Create a service called jekyll
• When you run that service, run jekyll serve --watch --incremental
• Map the container’s port 4001 to local port 4001
• Place the current directory (.) in the container’s file system at /srv/jekyll

Then I added an exclusion for this to my Jekyll _config.yml file:

port: 4001
exclude: [docker-compose.yml]
name: Bryan Slatner
job_title: Software Developer, Foodie, Cigar Lover

Now, I can simply type docker-compose up to have Jekyll start serving up my blog locally on port 4001.

Automating the Build and Deploy

I can finally automate the whole build and deploy process with a simple batch file:

docker-compose run jekyll jekyll build
fsi _scripts\deploy.fsx

This batch file uses docker-compose to run the Jekyll build inside the container. Since I’ve mapped my current directory to the container’s file system, the build output goes right where I expect it to. The deploy.fsx script is a simple script I wrote to compare the output of the previous build and the new build and upload the deltas to S3 for hosting.

That’s It

I blog a lot less than I’d like, but automating away all those mouse clicks and keystrokes means I might be more inclined to do more if it. I can only hope.

If all goes well, you’re now viewing this blog securely. Because nothing is more important than keeping your browsing of this blog safe from spying eyes.

I host this blog on AWS. It used to be served up directly from S3 static web hosting, but I’ve gotten all fancy and added:

• AWS CloudFront support, which should make it faster, because CDN and edge caching
• HTTPS
• Security headers

I used a cool Chrome plugin called Caspr Enforcer to test the Content-Security-Policy header before inflicting it on my adoring audience.

Doing this was an excellent, informative exercise because I have a number of Internet-facing web applications that really need to be properly using security headers. It also highlighted my addiction to inline styles and scripts, which you really shouldn’t be using.

Thanks to my old friend Julian Bucknall whose blog posts helped me through all of this.

This is part of a series of articles about how I’m trying to reform my bad keyboarding habits as a result of Repetitive Strain Injury. Other articles in this series can be found here. Other articles about demousification can be found here.

Google

TL;DR - Navigating through Google search results with the keyboard means hitting the Tab key over and over and over again.

I just went to Google and did a search for “Repetitive Strain Injury”. To go to the first search result requires hitting the Tab key 15 times.

That clearly sucks.

Fortunately, if you use Chrome or Firefox, there’s a great extension you can get that will allow you to navigate much better. I installed it immediately.

The Google Search Navigator extension for Chrome or Firefox makes it very easy to navigate search results with the keyboard. If you’re using Edge or Internet Explorer, you have my sympathies.

The first thing it gets right is that it immediately focuses the first search result, which is almost always what I want.

It has lots of keyboard shortcuts, but the main ones I’ll use are:

• Down (or J) to move to the next result
• Up (or K) to move to the previous result
• Enter to navigate to the result
• Ctrl+Enter to open the result in a new window

Other keys of note:

• Esc (or /) to go back to the search box
• A (or S) to go to the All tab
• I to go to the Images tab
• V to go to the Videos tab
• M to go to the Maps tab
• N to go to the News tab

It’s still pretty instinctual for me to reach for the mouse once the results display, but I’m getting over it. I’m not quite ready to actually remove the mouse from my desk, but that may be what it takes for me to really reprogram my brain.

This is part of a series of articles about how I’m trying to reform my bad keyboarding habits as a result of Repetitive Strain Injury. Other articles in this series can be found here. Other articles about demousification can be found here.

MOUSE BAD! BAD!!!

I’m addicted to mousing. I’m not sure how I became so dependent on it, considering how fast of a keyboardist I am. But admitting the problem is the first step on the path to recovery.

As I mentioned at the beginning of this series, one of the ways that I know I’ve had a productive day is if my right shoulder feels like it’s been stabbed by an angry monkey. The act of picking my hand up from the keyboard, moving it to the mouse, using the mouse, and moving my hand back again is rapidly becoming one of the most painful things I do each day. I may be one of the least athletic people you ever meet, but I frequently suffer from tennis elbow caused by too much mouse clicking.

Thus, one of my goals for mitigating my RSI is to reduce/eliminate as many trips to the mouse as I can.

This is easier said than done; the “point-and-click” interface is so ubiquitous that it’s very difficult to get away from. I’m embarassed to admit that just 30 seconds ago I moused my way through the source control pane in VS Code to commit a new script that I created for creating blog posts.

In fact, in most cases, unless a developer has spent a significant amount of time making sure that their interface is keyboard-friendly, it may be impossible or impractical to use that software using only the keyboard, despite the fact that Microsoft and Apple design guidelines explicitly state that software should be usable using only the keyboard. Most web sites – including all the ones I’ve ever written – fail in this regard.

Adding to the frustration is the fact that in many cases, figuring out how to navigate with the keyboard is obvious, but it isn’t at all obvious how to get to where you need to be. For example, from the message list in Outlook, how do you get to the list of folders so that you can navigate to another one?

So I’ve made a list of the sites and applications that I use most often and I’m committed to learning how to keyboard my way through them. That list is:

• Windows Explorer
• Standard Windows dialog boxes (file open, save, UAC prompts, etc.)
• Visual Studio
• Visual Studio Code
• JP Software’s Take Command (a command line replacement I’ve been using since the 80s)
• Outlook
• Excel
• Google
• Facebook
• Twitter
• Amazon.com

I imagine that things like Visual Studio will require several posts. I’m not feeling that ambitious yet, so I’m going to start where I can get the most bang for my buck and do a small series of posts on the web sites I use most often, starting with Google.

This is the second in a series of articles about how I’m trying to reform my bad keyboarding habits as a result of Repetitive Strain Injury. Other articles in this series can be found here.

I’ve been coding for about a week now using the Dvorak keyboard layout.

Sometimes, I just get super frustrated with how hard things are and I switch back to QWERTY and get shit done. It’s a bit like binge eating when on a diet.

When I get my ErgoDox EZ some of these problems will go away because I can customize the layout.

The first thing I’ve noticed is this: name any key on the QWERTY keyboard and I can hit it with either index finger without looking. This seems like such a stupid skill, but it’s amazing how many times each day I’ve been doing it. I can’t do it with the Dvorak layout, and this has been a huge source of slowdown for me. This comes up a lot when I notice a single character that needs to be changed. My normal workflow in this scenario is to click on the offending character, hit backspace with my right index finger, then tap the correct key with my index finger.

I suspect this is only one of many “brain macros” I’ve been executing over and over all day that I’m going to have to reprogram.

Another source of frustration has been with array indexes. Specifically, array index 0.

On the Dvorak layout, the two bracket keys are just to the right of the zero. To type [0], my right pinkie has to do this weird little dance where it hits the [, then one left to hit 0, then two to the right to hit ]. I don’t like it. It feels weird.

When I had my tonsils out, my doctor told me that there would come a point at which the pain would subside to the point that I’d be able to say “if it feels like this for the rest of my life, I can live with it.” It took me about two weeks to get to that point with my tonsils. I wonder how long it will take with the keyboard?

I’ve been programming professionally for 29 years. I’ve been typing as part of my job for 31.

As a result, I suffer from very bad Repetitive Strain Injury. I can directly measure how productive I’ve been during any given week by how badly my hands hurt on Friday evening. I’m left-handed, and my left hand suffers disproportionately. If I feel like my left hand was smashed by a hammer, I know I got a lot done.

I started learning to type long before I was given the opportunity to take a proper typing class. By the time a guidance counselor offered me a typing class in 12th grade, I could already type 120 words per minute.

But they were 120 words per minute typed the wrong way. I developed a lot of really bad habits. For one thing, I didn’t type with all my fingers. I only use three fingers on my right hand and two on my left for typing letters and numbers. I started typing on a keyboad where the function keys were on the left-hand side of the board. Because of that, and because most of the control keys I needed were also on the left-hand side, I developed the habit of contorting my left hand to type those keys. For example, to hit the keys for cut, copy, and paste, I hit the control key with my left thumb – tucking it under my hand – and hit the letter key with my left index finger. The area just below my left thumb is now almost constantly in pain, even when I’m not working.

Recently, I’ve been trying to develop better habits. But it is very difficult to work against 30+ years of muscle memory. When I’m programming “in the zone”, instinct takes over and I wind up doing all the wrong things again.

I’ve decided it’s time for a radical approach to this problem. If I’m going to work against 30 years of hard-forged neural pathways, I’m going to go all out.

Step 1: I’m going Dvorak. I have tried and failed to teach myself to type “properly” on a QWERTY keyboard. I constantly revert back to my weird self-taught style when I’m not paying attention. It’s super frustrating. So, I taught myself the Dvorak layout using all my fingers in the “proper” way. In fact, I’m typing this post in Dvorak mode. I can only type about 60 WPM this way – half my normal speed – but I feel like I’m getting better. Writing code in Visual Studio is another story: I’m constantly frustrated by needing to get things done and knowing I can go much faster.

Step 2: Ditching the mouse. I know I’ll never be able to get rid of it completely, but I need to find a way to reduce the number of times per day I reach for it. On days when I feel like my left hand has been smashed by a hammer, my right shoulder feels like it’s been stabbed by an angry monkey. This leads to…

Step 3: Learning to move around in Visual Studio with the keyboard. I like to code full screen, which means my Visual Studio window layout has most of the tool windows hidden. If I want to go to one of those, I’m always reaching for the mouse. I just learned that you can navigate between these windows by pressing Alt-F7 and Shift-Alt-F7. And I’ve learned that most of the windows I need all the time have a Ctrl-W combination that will take you there (e.g, Ctrl-W, O to go to the Output Window). Why did I never bother to learn this before? Oh, and if you’re focused in a tool window, pressing Ctrl-Tab or F7 will get you back to your code.

Step 4: I’m switching from my beloved Das Keyboard to an ErgoDox EZ keyboard. I picked this keyboard out of all of the choices available because:

• It’s a split configuration, so I can hold my hands shoulder width apart. This reduces tension in the shoulders and keeps me from having to have my wrists bent at an angle while typing.
• It has ortholinear keys, so my fingers don’t have to move in strange directions; they just need to go up and down.
• Its firmware is open source. We like open source.
• It’s completely programmable, so I can create weird keymaps that fit the way I work.
• I can create single, easy-to-reach keys that map to the most common hand-contorting key combinations that I use. For example, I reflexively hit Shift-Ctrl-S all the time to “Save All” in Visual Studio. Given how often I hit it, I’m going to replace that with a single key press.
• I can control the mouse with it.

Step 5: I’m going to try using Windows Speech Recognition where appropriate. I’m mostly using it in Outlook for typing e-mails. It doesn’t work so well for blog posts: I edit my blog in VSCode, and Speech Recognition isn’t quite as slick in there as it is in MS Office applications.

I still have 3 weeks to wait for the delivery of my ErgoDox EZ. I’m committed to doing most of my work using the Dvorak layout for those 3 weeks so that there’s less of a transition when it finally arrives.

I’m going to document all of the trials and tribulations of reprogramming my brain here. My goal is to be at my “normal” level of keyboarding speed within 6 months. I’ll let you know how that works out.

The Problem

There are exactly ten ways of selecting three from five, 12345:

123, 124, 125, 134, 135, 145, 234, 235, 245, and 345

In combinatorics, we use the notation, ⁵C₃ = 10.

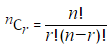In general, ,where r ≤ n, n! = n×(n−1)×...×3×2×1, and 0! = 1.

It is not until n = 23, that a value exceeds one-million: ²³C₁₀ = 1144066.

How many, not necessarily distinct, values of ⁿC_r, for 1 ≤ n ≤ 100, are greater than one-million?

The Solution

Thankfully, the problem definition has already given us the hard part of this problem. That is, figuring out the number of combinations for ⁿC_r.

The words "in general" in the problem definition made me nervous, but I couldn't think of any special cases that would apply here.

let rec fact n =
    match n with 
    | 0 -> 1I
    | 1 -> 1I
    | _ -> bigint(n) * fact (n-1)

let rec numCombos n r =
    fact n / ((fact r) * (fact (n - r)))

The numCombos function returns the number of combinations for a given n and r.

Now we can solve the problem:

seq {
    for n in 1..100 do
        for r in 1..n do
            yield (n,r)
}
|> Seq.map (fun (n,r) -> numCombos n r)
|> Seq.filter (fun n -> n > 1000000I)
|> Seq.length

The problem definition specifies 1 ≤ n ≤ 100. Therefore 1 ≤ r ≤ n because you can't take more from n than n.

We'll start by generating a sequence of all possible n paired with the possible r values for that n.

Next, we generate the number of combinations for each (n,r) pair.

Finally we filter out the values where the number of combos is more than one million and count them. That is the answer.

The Problem

It can be seen that the number, 125874, and its double, 251748, contain exactly the same digits, but in a different order.

Find the smallest positive integer, x, such that 2x, 3x, 4x, 5x, and 6x, contain the same digits.

The Solution

Now that we've passed problem 50, the problems start to get harder. I'm going to skip around a bit. I've gone directly from problem 50 to 52 because I haven't (yet) made my problem 51 solution sufficiently fast. But I'm getting there.

To solve this problem, the first thing we need is a function to determine if n times m contains the same digits as as n.

let checkMultiple (n : int) (ns : string) (m : int) =
    let multiple = (n * m).ToString()
    multiple.Length = ns.Length && 
    (ns |> Seq.forall (fun d -> multiple.IndexOf(d) >= 0))

The checkMultiple function takes a number, a string representation of that number, and a multiplier as input. It multiplies n * m and converts the result to a string. If that string has the same length as ns and contains all the same characters as ns, then we've found a match.

let isAnswer n =
    let ns = n.ToString()
    seq { 2..6 }
    |> Seq.forall (fun m -> checkMultiple n ns m)

The isAnswer function examines an n. If the checkMultiple function returns true for n multiplied by 2..6, then it returns true.

Now we can find the answer.

seq { 1..System.Int32.MaxValue }
|> Seq.find isAnswer

The Problem

The prime 41, can be written as the sum of six consecutive primes:

41 = 2 + 3 + 5 + 7 + 11 + 13

This is the longest sum of consecutive primes that adds to a prime below one-hundred.

The longest sum of consecutive primes below one-thousand that adds to a prime, contains 21 terms, and is equal to 953.

Which prime, below one-million, can be written as the sum of the most consecutive primes?

The Solution

Problem 50! I think after solving this one, I earn some sort of prize. I'm hoping for a luxury vacation, but I'm not holding my breath.

The first thing we need is the list of primes below 1000000. We'll start by stealing some code from problem 35 to generate those.

let intsqrt i = int(sqrt(float i))

let isPrime i =
    if i <= 1 then false
    elif i = 2 then true
    elif (i &&& 1) = 0 then false
    else
        let sr = intsqrt i
        seq { 3..2..sr } |> Seq.forall (fun f -> i%f<>0)

let rec nextPrime x =
    match x with
    | x when isPrime x -> x
    | x -> nextPrime (x + 1)


let getPrimesBelow max =
    let primeGenerator candidate =
        if candidate > max then
            None
        elif candidate = 2 then
            Some(2,3)
        else
            let next = nextPrime candidate
            if next >= max then
                None
            else
                Some(next,next+2)

    Seq.unfold primeGenerator 2

[<Literal>]
let target = 1000000

let primes = getPrimesBelow target |> List.ofSeq

Now we have a list of primes. The plan of attack is to go through each and find the starting prime of the sequence that, when summed, adds up to a prime number n.

let isSumOfConsecutivePrimes n =
    let rec isSum candidates sum len =
        match candidates with
        | [] -> None
        | x::xs ->
            let newSum = sum + x
            let newLen = len + 1
            if newSum = n then Some(newLen)
            elif newSum > n then None
            else
                isSum xs newSum newLen

    let rec findStartingPrime candidates =
        match candidates with
        | [] -> None
        | x::_ when x > n -> None
        | x::_ when x = n -> Some(n,1)
        | x::xs -> 
            match isSum xs x 1 with
            | Some l -> Some(n,l)
            | _ -> findStartingPrime xs

    findStartingPrime primes

isSumOfConsecutivePrimes starts by looping through each prime and determining if that prime is the start of the sequence we're looking for. The internal function isSum takes the list of subsequent primes, the current sum, and the length of the current sequence. If it gets to the end of the list of primes, it returns None. Otherwise, if it hits the sum we're looking for, it returns the length of the sequence that generated the sum.

This is a brute force way of solving the problem. I am certain there are other, better ways to do it. But this one works.

Full disclosure: in order to get this to run under the 1-minute time limit, I had to compile it with full code optimizations turned on. To get it to run in under a minute in FSI, I had to run it in parallel.

Here is the single-threaded code that returns the answer:

#time
primes
|> Seq.map isSumOfConsecutivePrimes
|> Seq.choose (fun x -> x)
|> Seq.maxBy (fun (_,len) -> len)
|> fst
#time

And here's the parallel version:

let isSumOfConsecutivePrimesAsync n = async {
    return isSumOfConsecutivePrimes n
}

#time
primes
|> Seq.map isSumOfConsecutivePrimesAsync
|> Async.Parallel
|> Async.RunSynchronously
|> Seq.choose(fun x -> x)
|> Seq.maxBy (fun (_,len) -> len)
|> fst
#time

The Problem

The arithmetic sequence, 1487, 4817, 8147, in which each of the terms increases by 3330, is unusual in two ways: (i) each of the three terms are prime, and, (ii) each of the 4-digit numbers are permutations of one another.

There are no arithmetic sequences made up of three 1-, 2-, or 3-digit primes, exhibiting this property, but there is one other 4-digit increasing sequence.

What 12-digit number do you form by concatenating the three terms in this sequence?

The Solution

First, let's write a function to generate a series of 3 numbers that increases by 3330.

let series n = [n; n+3330;n+3330+3330]

Next, we need a function to determine if all elements in a list contain exactly the same digits.

let haveSameDigits l =

    let first::others = 
        l 
        |> List.map (fun x -> x.ToString())

    let containsChar (c : char) (s : string) =
        s.IndexOf(c) >= 0

    let rec haveSame (others : string list) =
        match others with
        | [] -> true
        | x::xs ->
            if (first |> Seq.forall (fun c -> containsChar c x)) then
                haveSame xs
            else
                false

    haveSame others

The haveSameDigits function takes a list l as input. It starts out by finding the first term in the list and separating it from all the others. Then it calls the internal haveSame function which checks all the values in others to see if each other element contains all the digits in first.

Now we need a way to determine if all the elements in a list are prime.

let intsqrt i = int(sqrt(float i))

let isPrime i =
    if i <= 1 then false
    elif i = 2 then true
    elif (i &&& 1) = 0 then false
    else
        let sr = intsqrt i
        seq { 3..2..sr } |> Seq.forall (fun f -> i%f<>0)

let allArePrime l = 
    l |> List.forall isPrime

The allArePrime function returns true if all the elements in the input list l are prime. The functions intsqrt and isPrime are old friends from many other Euler problems.

Now we need a function to return a sequence of primes.

let rec nextPrime x =
    match x with
    | x when isPrime x -> x
    | x -> nextPrime (x + 1)

let getPrimesBelow max =
    let primeGenerator candidate =
        if candidate > max then
            None
        elif candidate = 2 then
            Some(2,3)
        else
            let next = nextPrime candidate
            if next >= max then
                None
            else
                Some(next,next+2)

    Seq.unfold primeGenerator 2

Again, the getPrimesBelow function is familiar if you've been following this series. We're going to use it to generate a sequence of 4-digit primes since we know from the problem definition that the value we're looking for has 4 digits.

For our last helper function, we need a simple way to concatenate together a list of integers, since that's the format required for the answer.

let listToString l = 
    System.String.Join("", l |> List.map (fun x -> x.ToString()))

Now we can solve the problem:

getPrimesBelow 10000
|> Seq.filter (fun n -> n > 1487)
|> Seq.map (fun n -> series n)
|> Seq.filter allArePrime
|> Seq.filter haveSameDigits
|> Seq.map listToString
|> Seq.head

We start by getting all primes below 10000 and then filtering out anything <= 1487. The problem definition gives us this starting point.

Next, we convert each element in the sequence into the series we're interested in. We filter out any of those series where not allArePrime and don't haveSameDigits.

And finally, we convert each element in the sequence to concatenated strings and return the head. That is the answer.