The Problem

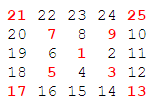
Starting with the number 1 and moving to the right in a clockwise direction a 5 by 5 spiral is formed as follows:

It can be verified that the sum of the numbers on the diagonals is 101.

What is the sum of the numbers on the diagonals in a 1001 by 1001 spiral formed in the same way?

The Solution

Full disclosure: when I originally solved this, I went about it all wrong. I was too focused on getting the answer and not focused enough on analyzing the problem.

My original solution had a complicated function that determined which way to move next based on current direction and position. It was a match statement with 9 different conditions. I was just learning to use F#'s active patterns and every solution looked like it needed active patterns to me. Here's what I came up with:

let size = 1001

type Direction = Up|Down|Left|Right

let getNextDirection (grid : int[,]) x y direction =
    match direction,x,y with
    | Left,x,_ when x = 0 -> Down
    | Left,x,y when grid.[x-1,y] <> 0 -> Down
    | Down,_,y when y = (size - 1) -> Right
    | Down,x,y when grid.[x,y+1] <> 0 -> Right
    | Right,x,_ when x = (size - 1) -> Up
    | Right,x,y when grid.[x+1,y] <> 0 -> Up
    | Up,_,y when y = 0 -> Left
    | Up,x,y when grid.[x,y-1] <> 0 -> Left
    | _ -> direction

I used the function above in a loop to "draw" the spiral and sum elements on the diagonals.

This is exactly the wrong approach. Here's a much better solution.

Each internal "ring" of the spiral forms a square with a side length of n. t is the total of the numbers in the previous ring. The numbers on the diagonals can all be expressed in terms of n and t. For example, when n is 3 and t is 1, then the 4 diagonals are:

• t+(n-1)*1 = 1+(3-1)*1 = 3
• t+(n-1)*2 = 1+(3-1)*2 = 5
• t+(n-1)*3 = 1+(3-1)*3 = 7
• t+(n-1)*4 = 1+(3-1)*4 = 9

The side length goes up by 2 each time. For the next side length, 5, we get:

• t+(n-1)*1 = 9+(5-1)*1 = 13
• t+(n-1)*2 = 9+(5-1)*2 = 17
• t+(n-1)*3 = 9+(5-1)*3 = 21
• t+(n-1)*4 = 9+(5-1)*4 = 25

The diagonals are all we care about, so we can ignore all the other numbers.

Knowing that, we'll first write a function to return the 4 diagonals for a given total and sideLength:

let diagonals total sideLength =
    let inc = sideLength - 1
    let dv n = total + inc * n
    [| 1..4 |] |> Array.map dv

Next, we construct a loop to keep calling diagonals and incrementing the sideLength until we get our answer.

let rec loop total sideLength diagonalSum =
    let newLength = sideLength + 2
    let diags = diagonals total newLength
    let newSum = diagonalSum + Array.sum diags
    if newLength = 1001 then
        newSum
    else
        loop diags.[3] newLength newSum

loop 1 1 1

The diagonals function returns the 4 diagonals for a given side length. The loop function figures out the next side length, gets its diagonals, and adds them to the sum. If we've hit a ring of side length 1001, it returns the total, otherwise it repeats the process.

Other Posts in This Series